Inverse Kinematics Trick
Inverse Kinematics

If you read my website, you probably know what inverse kinematics are already. I have a simple solution for a 1-joint that isn't the cosine method. I like it because it is easy to understand, although I don't think it's any faster.

Circle Trick

Suppose we have an arm or a leg with a single joint, that means it has:

  • 3 vertices (hip, knee, foot)
  • 2 edges (thigh and calf)
  • 1 joint (the knee)

Given a placement for the hip and the foot, we want to choose a natural placement for the knee.

Now let's make the somewhat obvious assumption that the thigh and calf don't change length as the joint moves. Then that means we can draw a circle with radius equal to the thigh length. The knee must be somewhere on the edge of this circle. We can do something similar with the calf and the foot.

That means the knee is somewhere on the edge of these two intersecting circles. Now all we have to do is a little bit of algebra, and find out where these two circles intersect. This isn't highschool, so I'm allowed to steal my answer from someone on the internet.

\(a = \frac{r_1^2 - r_2^2 + d^2}{2d}\)
\(h = \sqrt{r_1^2 - a^2}\)
\(x_3 = x_1 + \frac{a(x_2 - x_1)}{d}\)
\(y_3 = y_1 + \frac{a(y_2 - y_1)}{d}\)
\(x_4 = x_3 \pm \frac{h(y_2 - y_1)}{d}\)
\(y_4 = y_3 \mp \frac{h(x_2 - x_1)}{d}\)

In this demonstration, the "foot" is set to chase the mouse, and the hip is meant to stay where it is. That just leaves us to figure out the knee using the technique above.


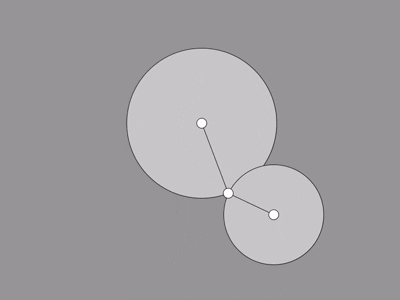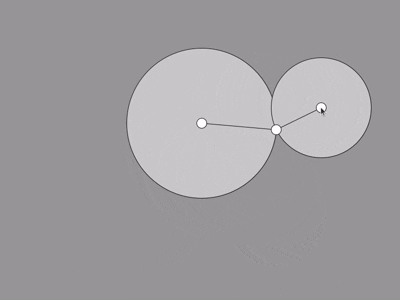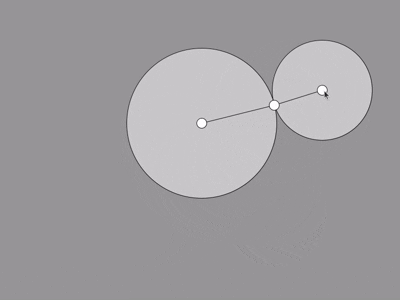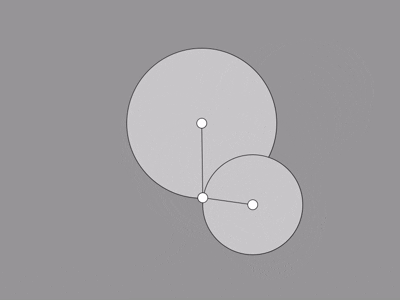
I think it works pretty well all things considered. Since there's usually two possible positions, we're always taking the one on the left. This is because most joints in animals don't bend both ways very well- so it looks weird.

Code
inverse_knee.pseudo
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void adjust_knee(hip, knee, foot, thigh_length, calf_length) {
    // Compute the distance between foot and hip.
    float d = sqrt( pow(foot.x - hip.x, 2) + pow(foot.y -hip.y, 2));

    // If the feet are too far away from the hips there's nothing we can do
    // we don't want to dislocate our critter's knee
    if (d > thigh_length + calf_length) return;
    else if (d == 0 && calf_length == thigh_length) return;

    // Pretend the thigh and calf are radii of two circles centered at the hip and foot
    // find the intersection of those circle (there should be one if we didn't return in
    // the above statement) and then put the knee on one of them.
    float dx = foot.x - hip.x;
    float dy = foot.y - hip.y;
    float a = (thigh_length * thigh_length - calf_length * calf_length + d * d) / (2 * d);
    float h = sqrt(thigh_length * thigh_length - a * a);
    float xm = hip.x + a * dx / d;
    float ym = hip.y + a * dy / d;
    float xs1 = xm + h * dy / d;
    float xs2 = xm - h * dy / d;
    float ys1 = ym - h * dx / d;
    float ys2 = ym + h * dx / d;

    // Finally we'll actually move the knee to one of the two positions.
    knee.x = xs2;
    knee.y = ys2;
}
Benefits Over The Law Of Cosines

This whole method is actually very round-about if you're familiar with The Law of Cosines technique. In fact I would say there aren't really any real benefits to implementing this design, with exception of some educational ones.

I think it's easier to understand how it works, and demonstrates "constraint design", where instead of listing how things should be we just come up with rules for how they can't be.

The last benefit I can think of for this example is that it doesn't require the user to input or parse any angles. So you don't need to worry about a reference line. That wasn't intentional, I just wasn't really thinking about angles when I came up with it.